Pi Day: Το π=3,14 σε μουσική!! Κάτι συγκλονιστικό που σίγουρα δεν έχετε ξαναδεί ... [Videos]
Η παγκόσμια σταθερά π=3,14 - Η πιο “διάσημη” μαθηματική σταθερά, εξαιτίας των ιδιοτήτων της, είναι η σταθερά π (όπως περιγράφεται στα ελληνικά από τη λέξη: περιφέρεια) ή Pi στα Λατινικά
![Pi Day: Το π=3,14 σε μουσική!! Κάτι συγκλονιστικό που σίγουρα δεν έχετε ξαναδεί ... [Videos]](https://static.mykonosticker.com/uploads/images/2021/05/image_750x_608eb13079fcf.jpg)
Η παγκόσμια σταθερά π=3,14
Η πιο “διάσημη” μαθηματική σταθερά, εξαιτίας των ιδιοτήτων της, είναι η σταθερά π (όπως περιγράφεται στα ελληνικά από τη λέξη: περιφέρεια) ή Pi στα Λατινικά. Η σταθερά απασχόλησε για πολλά χρόνια τους μαθηματικούς και τους φυσικούς και συνεχίζει να απασχολεί για τις εκπληκτικές ιδιότητες και την αρμονία που παρουσιάζει!!....
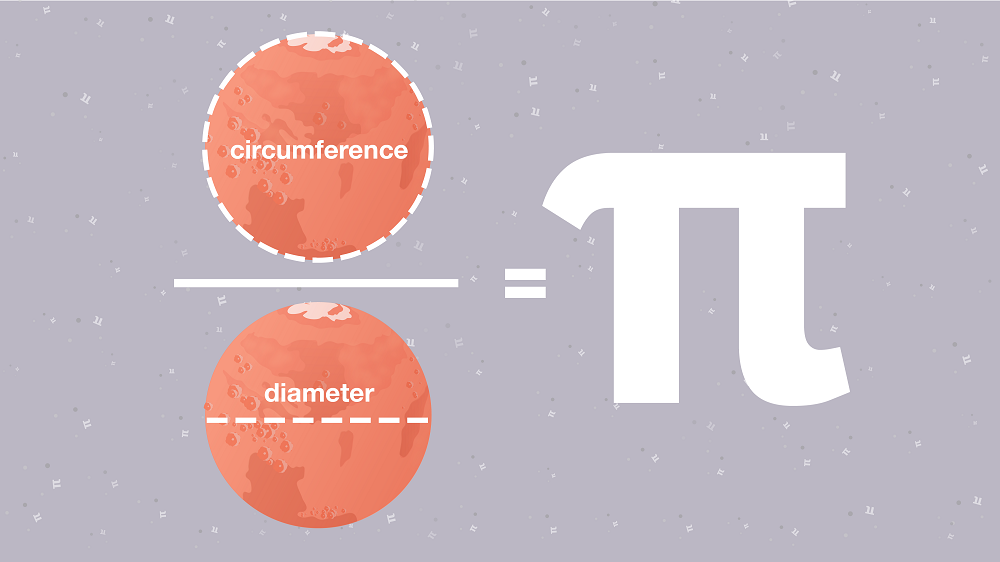
Η σταθερά π ισούται με το λόγο της περιφέρειας ενός οποιαδήποτε κύκλου προς τη διάμετρο του.
Όλοι οι κύκλοι ανεξαρτήτου διαμέτρου έχουν το ίδιο π και αυτό ισούται κατά προσέγγιση με 3,14.
Άλλοι επιστήμονες πάλι ορίζουν τη σταθερά pi ως την πλήρη στροφή που κάνει ένας κύκλος για να κυλίσει πάνω σε μια ευθεία γραμμή.
Απλά δείτε την παρακάτω εικόνα:
Όταν η διάμετρος του κύκλου είναι 1, η περιφέρειά του είναι ίση με π
Με αρκετές στρογγυλοποιήσεις (μάλλον άπειρες) το π ισούται με 3,14 όμως στην πραγματικότητα τα δεκαδικά του ψηφία είναι άπειρα και οι μαθηματικοί ακόμα μέχρι σήμερα δεν έχουν διαλευκάνει παρά μόνο μερικά από αυτά χρησιμοποιώντας μάλιστα τον πιο εξελιγμένο υπολογιστή στο κόσμο (που βρίσκεται στο Τόκιο).
Μερικά από τα πρώτα δεκαδικά ψηφία του πραγματικού αριθμού π φαίνονται στην παρακάτω εικόνα:

Μερικά από τα πρώτα δεκαδικά ψηφία του π
Όπως προανέφερα η σταθερά π έχει άπειρα ψηφία και ακόμα και με τον πιο ισχυρό υπολογιστή του κόσμου ανακαλύφθηκαν κάποια εκατομμύρια από αυτά χωρίς μάλιστα να μπορέσουν οι μαθηματικοί να βρουν κάποιο μοτίβο με το οποίο επαναλαμβάνονται αυτοί οι αριθμοί διότι παρουσιάζονται κάπως “τυχαία”. Βάζω τη λέξη τυχαία σε εισαγωγικά γιατί όπως θα διαπιστώσετε παρακάτω μόνο τυχαία δεν είναι γιατί η σταθερά αυτή παρουσιάζεται πολλές φορές στη φύση !!!
Η σταθερά π έχει δύο πολύ βασικές ιδιότητες
1. Καταρχήν είναι άρρητος αριθμός που σημαίνει ότι δεν μπορεί να εκφραστεί ως ο λόγος δύο ακέραιων αριθμών.
2. Έπειτα είναι υπερβατικός αριθμός πράγμα που σημαίνει ότι δεν υπάρχει πολυώνυμο με ρητούς συντελεστές του οποίου το π να αποτελεί ρίζα.
Συνέπεια αυτού είναι ότι η σταθερά π δεν μπορεί να κατασκευαστεί επομένως δεν μπορεί να τετραγωνιστεί ο κύκλος αφού για να τετραγωνίσουμε τον κύκλο θα πρέπει να έχουμε τη δυνατότητα να κατασκευάσουμε με κανόνα και διαβήτη τις συντεταγμένες των σημείων.
Επομένως είναι αδύνατο να κατασκευάσουμε ένα τετράγωνο με εμβαδόν ίσο με το εμβαδόν του αντίστοιχου κύκλου ( δλδ να τετραγωνίσουμε τον κύκλο).
Η σταθερά π δεν έχει συγκινήσει μόνο τους μαθηματικούς να ασχοληθούν μαζί της αλλά και απλούς ανθρώπους που προσπαθούν να εντυπωσιάσουν το κόσμο με το μυστήριο που κουβαλάει αυτή η σταθερά.
Μάλιστα έχουν γίνει αρκετές ταινίες με θέμα τη σταθερά π όπου οι πρωταγωνιστές προσπαθούν να την αποκρυπτογραφήσουν και να τη συνδέσουν με τη συμμετρία που υπάρχει στο κόσμο γύρω μας καθώς και με τον ίδιο το Θεό.
Ένα όμορφο αξιοσημείωτο “παιχνίδι” είναι ότι αν κάποιος ψάξει ανάμεσα στα άπειρα ψηφία του αριθμού π τότε ανάμεσα τους θα βρει τον αριθμό της ταυτότητας του, του διαβατηρίου, του τηλεφώνου του και γενικά οποιονδήποτε αριθμό…
Η σταθερά π είναι η σημαντικότερη σταθερά στα μαθηματικά, μια σταθερά που έχει παρατηρηθεί πολλές φορές στο κόσμο γύρω μας ακόμα και στο σύμπαν και γι αυτό το λόγο μερικοί την αποκαλούν σταθερά του σύμπαντος!!
Για παράδειγμα η ημερομηνία 28 Οκτωβρίου 1940 γραμμένη ως 28101940 παρουσιάζεται στο 7.641.792 ψηφίο της σταθεράς π!!!!
Η σπουδαιότητα της είναι τόσο μεγάλη που οι μαθηματικοί τη γιορτάζουν κάθε 14 Μαρτίου διότι τότε είναι 14/3 και σύμφωνα με τους Αμερικάνους που διαβάζουν πρώτα το μήνα και μετά τη μέρα 3/14 (όμως π=3,14).
Επίσης στην Ευρώπη τη γιορτάζουν και κάθε 22/7 αφού 22 δια 7 είναι 3,14. H ημέρα αυτή ονομάζεται Pi day προς τιμήν της σταθεράς!!
Δύο Αμερικανοί μαθηματικοί υπολόγισαν ότι το π έχει 1.120 ψηφία το 1949 με μια αριθμομηχανή γραφείου. Επί του παρόντος, το έχει υπολογιστεί να έχει 22.500.000.000.000 δεκαδικά ψηφία.
Επειδή όπως έχουμε αναφέρει τα ψηφία της σταθεράς είναι άπειρα , για το λόγο αυτό έχουν φτιαχτεί διάφοροι μνημονικοί κανόνες σε πολλές γλώσσες για να θυμόμαστε όσο το δυνατόν περισσότερα ψηφία.
(κλικ για μεγέθυνση)
Στα ελληνικά αρκετά γνωστό είναι το παρακάτω τετράστιχο το όποιο μας δίνει τα πρώτα 23 ψηφία: (περισσότερα εδώ:)
Αεί ο Θεός ο μέγας
γεωμετρεί το κύκλου μήκος
ίνα ορίση διαμέτρω
παρήγαγεν αριθμόν απέραντον και ον φευ!
ουδέποτε όλον θνητοί θα εύρωσι
Κλείνοντας, ήθελα να σας αναφέρω ότι εδώ παρουσιάζω μερικές μόνο από τις πληροφορίες που μπορείτε να βρείτε για τη σταθερά π.
Με μια αναζήτηση στο google να είστε σίγουροι ότι μπορείτε να βρείτε πολλές και εντυπωσιακές πληροφορίες. Απλά σας ρίχνουμε το δόλωμα......
Δε ξέρω πως μου ήρθε να γράψω για τη σταθερά αυτή. Κάποιον άκουσα να την αναφέρει και επειδή είχα ξαναασχοληθεί στο παρελθόν με αυτήν και επειδή, ως μαθηματικός, αγαπώ τα μαθηματικά αποφάσισα να κάνω μια ανάρτηση γι αυτήν, την αξίζει άλλωστε.
Παρακάτω, ένα τραγούδι για τη σταθερά μυστήριο, το π:
Τα Μαθηματικά του Αρχιμήδη, είναι μουσικά...???? Πόσο ακόμη θα συνεχίσει να μας εκπλήσσει η τεράστια γνώση που υπήρχε στην Αρχαία Ελλάδα?
Δείτε το Video, με την "θεία μελωδία" και θα μας καταλάβετε......
Η μέρα του αριθμού π - Δείτε γιατί γιορτάζει σήμερα η μαθηματική σταθερά
Ο αριθμός π είναι μια μαθηματική σταθερά που ορίζεται ως η περιφέρεια προς τη διάμετρο ενός κύκλου (π = C/d). Τα πρώτα δεκαδικά ψηφία που το αποτελούν είναι τα 3.14159265 και γι' αυτό κάθε χρόνο στις 14 Μαρτίου (3.14) γιορτάζεται η μέρα του π.
Οι άνθρωποι γνωρίζουν τον αριθμό π εδώ και χιλιάδες χρόνια, ενώ εμφανίζεται ακόμη και στην Αγία Γραφή, αλλά και σε αρχαίους πολιτισμούς: Οι Βαβυλώνιοι, οι αρχαίοι Έλληνες, ακόμα και οι Κινέζοι έχουν δοκιμάσει να υπολογίσουν όλο και πιο ακριβείς εκδόσεις του π.
Ο διάσημος μαθηματικός Αρχιμήδης προσπάθησε να δώσει έναν ακριβή υπολογισμό του π το 250 π.Χ. χρησιμοποιώντας δύο πολύγωνα 96 όψεων, ένα μέσα σε κύκλο και ένα δεύτερο έξω. Υποστήριξε ότι η τιμή του π θα βρίσκεται μεταξύ των μηκών της περιμέτρου του κάθε πολυγώνου. Η θεωρία του αυτή ήταν ο πιο ακριβής υπολογισμός του π για την εποχή.
Ωστόσο, χρόνια μετά, οι άνθρωποι υπολόγισαν το π με μεγαλύτερη ακρίβεια. Αλλά το κυνήγι για ακόμα περισσότερα δεκαδικά ψηφία έγινε επιτακτικό με την ανάπτυξη των ηλεκτρονικών υπολογιστών.
Οι άνθρωποι εκφράζουν την αγάπη τους για αυτόν τον μοναδικό αριθμό με διαφορετικούς τρόπους, απομνημονεύουν όσο πιο πολλά ψηφία του μπορούν (το πρόσφατο ρεκόρ είναι 67.890 δεκαδικά ψηφία) τρώνε πίτα ή συνθέτουν χαϊκού και τραγούδια.
Το 2009, το Κογκρέσο των ΗΠΑ, κήρυξε την 14η Μαρτίου ως Ημέρα του π με ψηφοφορία 391 υπέρ και 10 κατά.
Ακόμα και προμαχώνες της τριτοβάθμιας εκπαίδευσης γιορτάζουν με το δικό τους τρόπο. Το Ινστιτούτο Τεχνολογίας της Μασαχουσέτης δημοσιεύει αποφάσεις του κάθε 14 Μαρτίου και φέτος ειδικά το ανακοινώνουν στις 9.26π.μ.

Ακολουθούν 25 συναρπαστικά γεγονότα για το «π»:
- Το σύμβολο για το «π» χρησιμοποιείται εδώ και πάνω από 250 χρόνια. Το σύμβολο εισήχθη από τον William Jones, έναν Ουαλό μαθηματικό, το 1706. Το σύμβολο έγινε δημοφιλές από τον μαθηματικό Leonhard Euler.
- Δεδομένου ότι η ακριβής τιμή του π δεν μπορεί ποτέ να υπολογιστεί, δεν μπορούμε ποτέ να βρούμε το ακριβές εμβαδόν ή την περιφέρεια ενός κύκλου.
- Η 14η Μαρτίου ή 3/14 γιορτάζεται ως ημέρα του «π» επειδή τα 3,14 είναι τα πρώτα ψηφία του «π». Οι σπασίκλες των μαθηματικών σε όλο τον κόσμο λατρεύουν να γιορτάζουν αυτόν τον απείρως μακρύ, ατελείωτο αριθμό.
- Το ρεκόρ για την απαγγελία του μεγαλύτερου αριθμού δεκαδικών ψηφίων του «π» επιτεύχθηκε από τον Rajveer Meena στο Πανεπιστήμιο VIT στο Vellore της Ινδίας στις 21 Μαρτίου 2015. Κατάφερε να απαγγείλει 70.000 δεκαδικά ψηφία. Για να διατηρήσει την ιερότητα του ρεκόρ, ο Rajveer φορούσε μαντήλι στα μάτια καθ’ όλη τη διάρκεια της ανάκλησής του, η οποία διήρκεσε εκπληκτικές 10 ώρες! Δεν μπορείτε να το πιστέψετε; Λοιπόν, ορίστε οι αποδείξεις.
- Το «π» είναι στην πραγματικότητα μέρος της αιγυπτιακής μυθολογίας. Οι άνθρωποι στην Αίγυπτο πίστευαν ότι οι πυραμίδες της Γκίζας χτίστηκαν με βάση τις αρχές του «π». Το κάθετο ύψος των πυραμίδων έχει την ίδια σχέση με την περίμετρο της βάσης τους όπως η σχέση μεταξύ της ακτίνας ενός κύκλου και της περιφέρειας του. Οι πυραμίδες είναι πρωτοφανείς κατασκευές και αποτελούν ένα από τα επτά θαύματα του κόσμου.
- Ο φυσικός Larry Shaw άρχισε να γιορτάζει την 14η Μαρτίου ως ημέρα του «π» στο επιστημονικό μουσείο Exploratorium του Σαν Φρανσίσκο. Εκεί είναι γνωστός ως ο πρίγκιπας του «π».
- Υπάρχει μια ολόκληρη γλώσσα φτιαγμένη από τον αριθμό «π». Όμως, πώς είναι δυνατόν αυτό; Λοιπόν, κάποιοι άνθρωποι αγάπησαν το «π» τόσο πολύ ώστε να εφεύρουν μια διάλεκτο βασισμένη σε αυτό. Στα “Pi-lish” ο αριθμός των γραμμάτων σε κάθε λέξη αντιστοιχεί στο αντίστοιχο ψηφίο του «π». Αυτή η πρώτη λέξη έχει τρία γράμματα, η δεύτερη έχει ένα γράμμα, η τρίτη έχει τέσσερα γράμματα κ.ο.κ. Αυτή η γλώσσα είναι πιο δημοφιλής από ό,τι νομίζετε. Ο μηχανικός λογισμικού Michael Keith έγραψε ένα ολόκληρο βιβλίο, με τίτλο Not a Wake σε αυτή τη γλώσσα.
- Το «π» δεν ήταν πάντα γνωστό ως «π». Πριν από τη δεκαετία του 1700, οι άνθρωποι αναφέρονταν στον αριθμό που γνωρίζουμε ως «π» ως «το μέγεθος που όταν η διάμετρος πολλαπλασιάζεται με αυτό, δίνει την περιφέρεια». Δεν αποτελεί έκπληξη το γεγονός ότι οι άνθρωποι κουράστηκαν να λένε τόσα πολλά κάθε φορά που ήθελαν να μιλήσουν για το «π». Ο Ουαλός μαθηματικός William Jones, φίλος του Sir Isaac Newton, άρχισε να χρησιμοποιεί το σύμβολο για το «π» το 1706.
- Ποτέ δεν θα μπορέσουμε να βρούμε όλα τα ψηφία του π, λόγω του ίδιου του ορισμού του ως ανορθολογικού αριθμού. Ο βαβυλωνιακός πολιτισμός χρησιμοποιούσε το κλάσμα 3 ⅛, οι Κινέζοι χρησιμοποιούσαν τον ακέραιο αριθμό 3. Μέχρι το 1665, ο Ισαάκ Νεύτων υπολόγισε το πι με 16 δεκαδικά ψηφία. Οι υπολογιστές δεν είχαν εφευρεθεί ακόμα, οπότε αυτό ήταν μια πολύ μεγάλη υπόθεση. Στις αρχές της δεκαετίας του 1700 ο Τόμας Λάγκνεϊ υπολόγισε 127 δεκαδικά ψηφία του πι, επιτυγχάνοντας νέο ρεκόρ. Στο δεύτερο μισό του εικοστού αιώνα, ο αριθμός των ψηφίων του «π» αυξήθηκε από περίπου 2000 σε 500.000 στον CDC 6600, έναν από τους πρώτους υπολογιστές που κατασκευάστηκαν ποτέ. Το ρεκόρ αυτό καταρρίφθηκε και πάλι το 2017, όταν ένας Ελβετός επιστήμονας υπολόγισε περισσότερα από 22 τρισεκατομμύρια ψηφία του π. Ο υπολογισμός διήρκεσε πάνω από εκατό ημέρες.
- Η χρησιμότητα του «π» έχει αποτελέσει αντικείμενο συζήτησης, αν και έχει αγαπηθεί από πολλούς λάτρεις των μαθηματικών. Κάποιοι πιστεύουν ότι το ταυ (που ισούται με 2π) είναι πιο κατάλληλο για υπολογισμούς κύκλων. Για παράδειγμα, μπορείτε να πολλαπλασιάσετε το «ταυ» με την ακτίνα του «α» για να υπολογίσετε την περιφέρειά του πιο διαισθητικά. Το «ταυ4» αντιπροσωπεύει επίσης τη γωνία ενός τετάρτου ενός κύκλου.
- Στο επιστημονικό μουσείο Exploratorium, μια κυκλική παρέλαση γίνεται κάθε χρόνο την ημέρα του «π». Κάθε άτομο που συμμετέχει κρατάει ένα ψηφίο του αριθμού «π». Δεν γιορταζόταν σε όλες τις Ηνωμένες Πολιτείες όπως τώρα, μέχρι που το Κογκρέσο ψήφισε το ψήφισμα 224, το οποίο όρισε την 14η Μαρτίου ως ημέρα του «π». Το Κογκρέσο ήλπιζε ότι ο εορτασμός της ημέρας του «π» θα καλλιεργούσε μεγαλύτερο ενθουσιασμό για τα μαθηματικά και τις επιστήμες στους Αμερικανούς μαθητές.
- Ο υπολογισμός του «π» είναι μια δοκιμασία καταπόνησης για έναν υπολογιστή. Λειτουργεί ακριβώς όπως ένα ψηφιακό καρδιογράφημα, αφού δείχνει το επίπεδο δραστηριότητας εντός του επεξεργαστή του υπολογιστή.
- Η εταιρεία Givenchy πουλάει μια ανδρική κολόνια με το όνομα “Pi”. Η εταιρεία εμπορεύεται το προϊόν αυτό ως ικανό να ενισχύσει την ελκυστικότητα των ευφυών και οραματιστών ανδρών.
- Ο αριθμός «π» δεν αποτελεί απλώς σημαντικό μέρος των συζητήσεων μεταξύ μαθηματικών ή φοιτητών. Στη διάσημη δίκη του O.J. Simpson, η επιχειρηματολογία του δικηγόρου υπεράσπισης και του πράκτορα του FBI περιστράφηκε γύρω από την τιμή του «π». Τα ευρήματα του πράκτορα του FBI στην υπόθεση δεν ήταν ακριβή επειδή χρησιμοποίησε λανθασμένα το «π».
- Ο αριθμός «π» ήταν τόσο γοητευτικός, ακόμη και τον 16ο αιώνα, ώστε ο Ολλανδός γερμανικής καταγωγής μαθηματικός Ludolph van Ceulen πέρασε το μεγαλύτερο μέρος της ζωής του υπολογίζοντας τα πρώτα 36 ψηφία του «π». Λέγεται ότι οι πρώτοι 36 αριθμοί ήταν χαραγμένοι στην επιτύμβια στήλη του, η οποία έχει πλέον χαθεί.
- Ο William Shanks, ένας Βρετανός μαθηματικός, εργάστηκε με το χέρι για να βρει τα ψηφία του «π» το 1873. Πέρασε πολλά χρόνια προσπαθώντας να υπολογίσει τα ψηφία του «π» με το χέρι και βρήκε τα πρώτα 707 ψηφία. Δυστυχώς, το 527ο ψηφίο που βρήκε ήταν λάθος, γεγονός που έβγαλε λάθος και όλα τα επόμενα ψηφία.
- Το έτος 1888, ένας επαρχιακός γιατρός από την Ιντιάνα ισχυρίστηκε ότι είχε μάθει το ακριβές μέτρο ενός κύκλου με υπερφυσικά μέσα. Πίστευε τόσο πολύ στις «υπερφυσικές» του γνώσεις, ώστε κατέθεσε πρόταση να περάσει ένα νομοσχέδιο στο νομοθετικό σώμα της Ιντιάνα, ώστε να μπορεί να κατοχυρώσει τα πνευματικά δικαιώματα των ιδιοφυών ευρημάτων του. Ωστόσο, υπήρχε ένας καθηγητής μαθηματικών στο νομοθετικό σώμα που έδειξε στον συνάδελφο πώς το προτεινόμενο νομοσχέδιο του θα οδηγούσε σε λάθος τιμή του «π».
- Ο αριθμός «π» είναι κυριολεκτικά άπειρα μεγάλος. Όμως, ο αριθμός 123456 δεν εμφανίζεται πουθενά στο πρώτο εκατομμύριο ψηφίων του «π». Είναι λίγο παράξενο, διότι αν σε ένα εκατομμύριο ψηφία του «π» δεν υπάρχει η ακολουθία 124356, τότε σίγουρα είναι ο πιο μοναδικός αριθμός.
- Οι Κινέζοι ήταν πολύ πιο μπροστά από τη Δύση στην εύρεση των ψηφίων του «π». Γιατί; Οι Κινέζοι μαθηματικοί ήταν μπροστά στο παιχνίδι του «π» για δύο λόγους: είχαν δεκαδικούς συμβολισμούς και είχαν ένα σύμβολο για τον αριθμό μηδέν. Μόνο στα τέλη του Μεσαίωνα οι Ευρωπαίοι μαθηματικοί άρχισαν να χρησιμοποιούν τον αριθμό μηδέν. Εκείνη την εποχή, οι Ευρωπαίοι μαθηματικοί συνεργάστηκαν με αραβικά και ινδικά μυαλά για να φέρουν το σύμβολο του μηδενός στο σύστημά τους.
- Στην αρχαιότητα, οι μαθηματικοί χρησιμοποιούσαν μια μοναδική μέθοδο για τον υπολογισμό του «π». Προσέθεταν όλο και περισσότερες πλευρές σε ένα πολύγωνο, ώστε το εμβαδόν του να πλησιάζει το εμβαδόν ενός κύκλου. Ο Αρχιμήδης, ο πιο διάσημος Έλληνας μαθηματικός και εφευρέτης, χρησιμοποίησε ένα πολύγωνο με 96 πλευρές. Πολλοί άλλοι μαθηματικοί χρησιμοποίησαν επίσης αυτήν την πολυγωνική μέθοδο για να υπολογίσουν τον απείρως μεγάλο αριθμό «π». Στην Κίνα, ένας μαθηματικός χρησιμοποίησε πάνω από 3.000 πλευρές σε ένα πολύγωνο για να καταλήξει στην τιμή 3,14159. Ένας άλλος μαθηματικός χρησιμοποίησε περίπου 25.000 πλευρές για να υπολογίσει το «π».
- Πολλοί μαθηματικοί πιστεύουν ότι είναι πιο ακριβές να πούμε ότι ένας κύκλος έχει άπειρες γωνίες παρά ότι δεν έχει καμία. Είναι λογικό να υποθέσουμε ότι ο άπειρος αριθμός των γωνιών ενός κύκλου συσχετίζεται με τον άπειρο αριθμό των ψηφίων του «π».
- Ο αριθμός «π» είναι πολύ αποτελεσματικός όταν χρησιμοποιείται σε υπολογισμούς. Για παράδειγμα, η στρογγυλοποίηση του αριθμού «π» σε μόλις 9 ψηφία μετά το δεκαδικό και η χρήση του για τον υπολογισμό της περιφέρειας της γης δίνει απίστευτα ακριβή αποτελέσματα. Για κάθε 25.000 μίλια, ο αριθμός «π» θα σφάλει μόνο στο 1/4 της ίντσας – (0,63,5 του εκατοστού)
- Ακόμα και σήμερα, οι άνθρωποι αγωνίζονται να υπολογίσουν περισσότερα ψηφία του «π» σε έναν ατελείωτο διαγωνισμό. Το έτος 2010, ένας Ιάπωνας μηχανικός και ένας Αμερικανός μάγος υπολογιστών έσπασαν το ρεκόρ για τον μεγαλύτερο αριθμό ψηφίων του «π», υπολογίζοντας μέχρι και 5 τρισεκατομμύρια ψηφία του «π». Το εκπληκτικό είναι ότι δεν χρησιμοποίησαν υπερυπολογιστές. Χρησιμοποίησαν απλώς επιτραπέζιους υπολογιστές, 20 εξωτερικούς σκληρούς δίσκους και το λαμπρό μυαλό τους.
- Το ελληνικό γράμμα «π» είναι το πρώτο γράμμα της λέξης περιφέρεια και περίμετρος. Και όπως όλοι γνωρίζουμε, το «π» είναι ο λόγος της «περιφέρειας» ενός κύκλου προς τη διάμετρό του.
- Είναι ενδιαφέρον ότι ο ένας από τους πιο διάσημους επιστήμονες στον κόσμο έχει σχέση με την ημέρα του «π», όπως ο Άλμπερτ Αϊνστάιν γεννήθηκε στις 14 Μαρτίου 1879.










![Καλά Κούλουμα και Καλή Σαρακοστή!!! [Video]](https://static.mykonosticker.com/uploads/images/2021/05/image_380x226_608ed797a99a4.jpg)













![Καλά Κούλουμα και Καλή Σαρακοστή!!! [Video]](https://static.mykonosticker.com/uploads/images/2021/05/image_140x98_608ed797ba176.jpg)


